A shallow dive into Cellular Automata
Cellular Automatas
Inspired by Stephen Wolfram's book, which I finally got around reading now under lockdown, I decided to spend my week trying an experiment with Cellular Automata (CA) and crypto markets. My hope was that there was some sort of pattern matching with a CA rule in the minute to minute movement. Markets are interesting because, while not quite Turing Complete, they do seem to follow the law of Computational Irreducibility, which states the only way to determine the answer to a computationally irreducible question is to perform, or simulate, the computation.
I won't dwell too much on what a CA is, there are other way better sources explaining that. But if you've ever seen one of those pictures or played Conway's Game of Life, those are CAs.
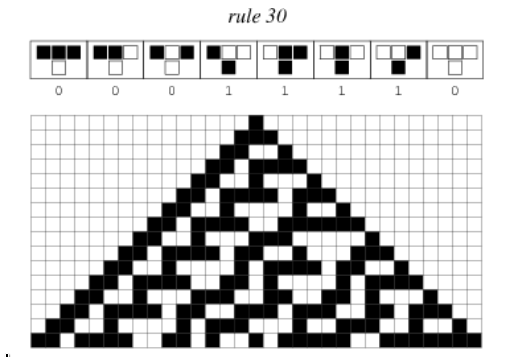
They're essentially abstract computational systems that can be used as models for complexity. A lot of CA results can be found in nature. For more info I'd greatly recommend reading a New Kind of Science, freely available on the internet. Back to the topic of markets, I had hoped that, as movement over larger periods of time can be attributed to rational actions and reactions, movement on a minute by minute basis could've matched some CA rule. Excerpt from A New Kind of Science

So I wrote some code to take various increments of the minute to minute movement and generate all CA rules with that size and find matches. As an example, taking 30 minutes of market data meant generating all CAs with a width of 30 and depth 10.000, changing the market data to 1s and 0s (1 if the price went up, 0 if the price went down), and then trying to identify matches. And while I've been able to find matches, especially in rule 45 that happened to contain all the market data if split in increments up to 20 minutes, they're completely random and follow no set pattern. I've tried plugging the results into https://oeis.org but still didn't get anything. For the most part I avoided using any of the rules that involved a high degree of randomness, such as rules part of class 4 (rule 110) and class 3 (rule 30, 90, 135, 184).
So, the results are that I didn't find anything. Or to be more scientific, I failed to reject the null hypothesis. And that's a good thing, because in retrospect I realized that my hypothesis was flawed, at least a degree. CAs are defined by the rules that instruct the cells how to act. I aimed for a low hanging fruit by simply attempting to find a CA that would match market data by brute forcing possibilities. Instead, as someone more observant than I am pointed out, I think I should've focused on formulating the market as a CA. To move away from the crypto space, let's consider that many raw materials are priced in dollars. U.S. Dollar depreciation typically increases the price of raw materials while a dollar appreciation decreases commodity prices. More details on investopedia. Letss also add the S&P500 into the mix as a barometer for the health of the market. Here, the rising prices of commodities would lead people away from the stock market, and the inverse would apply too. Let's put it into a CA format:

Appreciating dollar lowers material price and increases commodity price:

Probably not the best examples as all the values are too anchored to the dollar, but I hope it sketches out the idea a bit. I do intend to investigate this further at some point, but for now I'm taking a break to focus on my pentesting duties. Regardless, let's move on to what I learned.
Lessons learned
Cellular Automata, Cellular Automaton and Multithreading
I did learn how to generate them and what makes them work, although I took a shortcut after generating the first 5 rules and used an already existing project on github: Cellpylib. In order to save time, I used that project to generate all the relevant CA rules in a 100 x 100.000 matrix. This took about 10 hours on an overclocked 8th gen i5 with multithreading turned to use all 6 cores. The global interpreter lock is a bit annoying but the multiprocessing lib helps to a large degree. It did, however, make me reconsider my skill set, as my main programming language - Python and my secondary one - JS, while immensely useful for my day to day job, have their drawbacks. Actually JS has a lot of drawbacks but I won't going to get into that now.Caching, GPU programming and numpy
I was fortunate enough that the cached_property library has been added to the functools standard library in python3.8. While I started by just reading and writing to the previously generated rules, this system stopped working once I attempted to move the code to the GPU with numba. Numba doesn't support i/o operations in the traditional sense, so I had to resort to caching. While numba still strives to maintain the python spirit of not having to explicitly declare data types and structures, this can severely affect performance or straight up prevent you from compiling your functions. To avoid those issues, I had to preload and cache all my rules, convert my parket data to numpy arrays and avoid any string operations. So instead of using
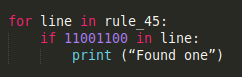
I had to use something like
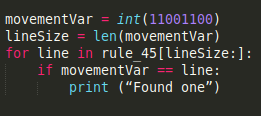
To anyone used to working in lower level languages, this probably seems trivial, but to someone used to flinging code fast and optimizing later, this was a bit tedious.
Overall, I think I used my time to learn some useful concepts, and I'll definitely be returning to this topic in the future.
Cool, where's the code?
As the project was very rushed, the code is not quite up to par. Since I intend to come back to this project, I will update it and put it on my github. Yes, I know I'm breaking the rule of "Less talk, show me code". I'm a bit short on time, as around this time I was supposed to learn and practice Active Directory pen testing, but I decided to take this detour to test an idea.